9. An experiment to test the validity of the Mach principle.

The Mach principle means that when approaching a massive body, the laws of physics must change. Change in dimensional physical constants,
the dielectric, magnetic, gravitational wave and Planck constant when approaching a massive body and means that when approaching a massive body
but the laws of physics change. Since the numerical values of these constants are interrelated, it is sufficient to show experimentally that gravity
changes one of these constants, which means that the numeric values of the other constants will also change accordingly.
In my opinion, Planck's constant is best suited for this role. A change in the Planck constant automatically means a change in the dielectric and
magnetic constant, since

where

Moreover, the dielectric and magnetic constants must change so that the speed of light remains constant.
And so that the ratio of the electric repulsion force of two protons or electrons remains unchanged, inversely proportional to
the dielectric constant must change the gravitational constant.


Next, we consider an experimental setup that can be used to check the variability of the Planck constant depending on
from the gravitational potential.

At the top of the mountain and at its foot, a pair of identical photocells with cathodes to each other is installed.
In each pair, the cathode of one of the cells irradiated with a laser of frequency f1, and the other photocell laser catatau f2.
Due to the photoelectric effect, in accordance with Stoletov's law, a voltage will occur between the anodes in each pair

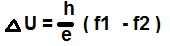
If the measured value of these voltages at a pair of solar cells at the foot of the mountain is less than that of the solar cells at the top of the mountain, then this is .
will mean that at the top of the mountain, the Planck constant is greater than at the bottom of the mountain.
Voltmeters for measuring these voltages should be installed at the same level in the middle of the mountain to exclude the influence of gravitational
potential on the voltmeter readings. The main difficulty of this experiment is that these voltages should be measured with a very high
accuracy, on the order of 10^-14. This accuracy can be achieved if you make measurements with voltmeters arranged as follows

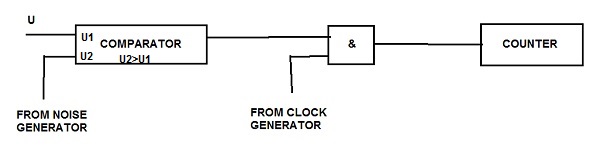
The measured voltage is applied to one of the inputs of the comparator, the other input is fed slkchayny noise.
If the measured voltage is greater than the noise voltage, then the pulse from the clock generator passes to the counter, but if it is greater than
the voltage of the noise, then the pulse on the counter does not pass. Thus, the probability of passing the pulse of the clock generator to the counter
the higher the measured voltage is, the higher the measured voltage, and for a sufficiently long measurement period (mex, year), the required
can be achieved. the accuracy of measurements.