13. The fall of the apple and the LC oscillatory circuit in the reference frame of the remote observer.

Let's do a thought experiment. A tree grows on planet X, an apple falls from it from a height H. There is an observer next to the tree,
and in his frame of reference, the apple will fall in time

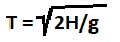
Let another observer from outer space also observe the fall of an apple through a telescope. Due to the fact that the second observer is < br /> in a weaker gravity, in its frame of reference, the time of the apple's fall will be slowed down by a factor of k, and the height of H will also be increased by a factor of k.










This shows that in order for the acceleration of free fall on the surface of planet X in sesame starting a remote observer g' would be k times
less than it is in the system of reference of the observer insider, requires that the gravitational constant G in the reference frame of an external observer would also
k times greater than in the reference system of nablyudala insider. Otherwise, in the reference frame of the remote observer, the acceleration of gravity g' will not be in k, but in k^2
times less than it is in the frame of reference of the insider observer.


This simple thought experiment proves that in the reference frame of a remote observer, the gravitational constant must change back
proportional to the change in the distance/time scale. This means that there are no black holes, more about this here.

For those who still do not believe that the numerical value of the gravitational constant in the reference frame of a remote observer changes back
in proportion to the change in the time/distance scale, I propose to solve the following problem.
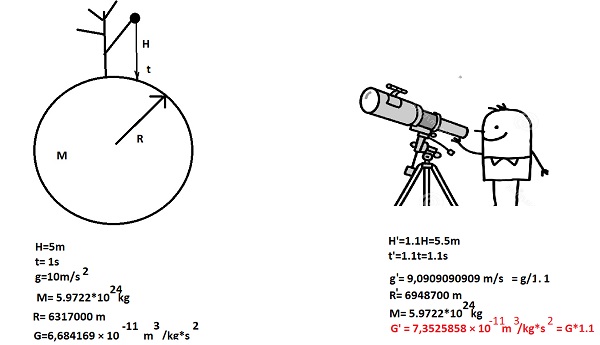
On a planet with a mass of 5.95*10 ^ 24 kg, a radius of 6317000 m, an apple falls from a tree from a height of 5 m in 1 second, calculate the value of the gravitational < br /> constant G. And then calculate the value of the gravitational constant G' in the reference frame of the remote observer, in which the apple falls
for 1.1 seconds from a height of 5.5 m and the radius of the planet is 6948700, respectively, and compare the obtained values of G and G'.

Next, we consider the LC oscillatory circuit. The capacity of the codensator in the frame of reference of the insider observer is calculated by the formula.

First, let's see how the capacitance of the capacitor will change in the reference frame of the remote observer, if we assume that the dielectric constant on changes.
In the reference frame of an external observer, the area of the capacitor plates will increase by k^2 times, and the distance between the plates will also increase by k times,
thus, the capacitance of the capacitor will increase by k times.
Next, let's see how the inductance of the coil will change in the reference system of the remote observer, which is in the reference system of the insider observer
it is calculated by the formula.

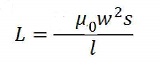
First, let's see how the capacitance of the capacitor will change in the reference frame of the remote observer, if we assume that the dielectric constant on changes.
In the reference frame of an external observer, the area of the capacitor plates will increase by k^2 times, and the distance between the plates will also increase by k times,
thus, the capacitance of the capacitor will increase by k times.
Next, let's see how the inductance of the coil will change in the reference system of the remote observer, which is in the reference system of the insider observer
it is calculated by the formula.

We see that the oscillation period increases by k times, as it should be.
But the dimension of the electric constant F/m, sldovatelno in the reference frame of a remote observer, it should decrease by k times,
then, in order for the speed of light to remain constant, the magnetic constant must increase by k times.
Then, in the reference frame of the remote observer, the capacitance of the capacitor will not change, but the inductance of the coil will increase by k^2 times.
Thus, the oscillation period of the oscillating circuit will also increase by k times in this case.


To find out which of these two options is correct, we will introduce an active resistance into the oscillatory circuit
so that the fluctuations in it become attenuated.
Let's see how the resistance value changes when switching to the reference system of a remote observer. Resistance is the ratio
the difference of electrical potentials to the current strength in the conductor. The dimension of the electric potential is Joule/Coulomb.
The joule does not change when the time/distance scale changes synchronously, and the Сoulomb is not related to the time/distance scales at all,
therefore, the difference of electrical potentials in the reference system of the remote observer will be the same as in the reference system
an insider's observer. The strength of the electric current in the conductor is equal to the ratio of the charge that has passed through the cross-section of the conductor to the time
for which this charge passed. The charge in the reference frame of the external observer will be the same as in the reference frame of the insider observer
but the time will increase by k times.
Thus, the resistance in the reference frame of the remote observer will be k times greater than in
the reference frame of the insider observer.

In order for both the insider observer and the remote observer to see the same picture of damped oscillations on different time scales,
it is required that the Q-factor of the oscillatory circuit in the reference systems of both observers would be the same.
(Q-factor is a parameter of the oscillatory system that determines the resonance width and characterizes,
how many times are the energy reserves in the system greater than the energy losses during the phase change by 1 radian.)

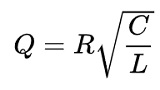
In the first variant, when the dielectric and magnetic constants are considered unchanged, in the reference frame of the remote observer, the Q-factor
the oscillating circuit will be

And in the second variant, when the dielectric and magnetic constants change in different directions by k times, in the reference frame of the remote observer
the Q-factor the oscillating circuit will be

Thus, this thought experiment with an oscillatory circuit shows that in the reference frame of a remote observer, the dielectric and magnetic constants must change in different directions in accordance with the change in the time/distance scale. Then it is not difficult to show
that the Planck constant will also change in the reference frame of the remote observer, since it is equal to