Почти век назад Хабблом было открыто, что Вселенная расширяется и что скорость удаления галактик друг от друга пропорционально расстоянию между ними.
В 1998 в процессе наблюдения за вспышками сверхновых в дальних галактиках было сделано еще более шокирующее открытие,
Вселенная, оказывается, расширяется еще быстрее, чем предсказывает Закон Хаббла.
Это ускоренное расширение Вселенной приписали действию некой «темной энергии»,
которая растет и даже может разорвать все атомы во Вселенной на части.
В этой главе я попытаюсь объяснить, что же это за «темная энергия»,
что в ней нет ничего сверхъестественного и что все происходит в соответствии с Законом Сохранения Энергии.
Попробуем разобраться с вопросом «почему расширяется Вселенная» и где источник энергии её расширения.
Рассмотрим систему из двух галактик A и B, распоженных на расстоянии R.
Вспомним общеизвестную из ядерной физики формулу для массы ядра, которая равна сумме масс протонов и нейтронов за минусом энергии связи, деленной на
квадрат скорости света, и запишем аналогичную формулу для массы системы из двух галактик.
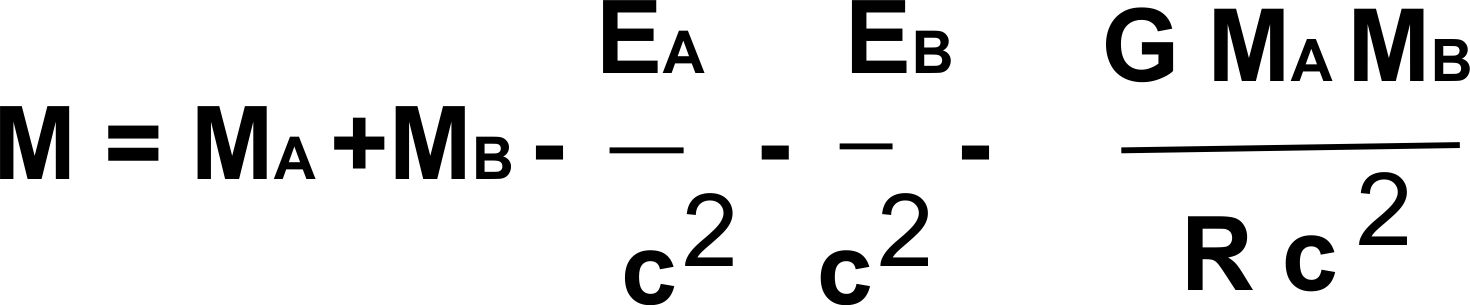
В этой формуле Ma и Mb - массы галактик A и B cоответственно, Ea и Eb - внутренние энергии гравитационной связи в галактиках соответственно,
G - гравитационная постоянная, c - скорость света. Последнее слагаемое в этой формуле выражает гравитационную энергию связи между галактиками,
оно записано исходя из классической Ньтоновской модели гравитации.
Закон сохранения энергии требует, что если галактики сожмутся, то есть увеличатся гравитационные энергии связи Ea и Eb, то это должно быть
скомпенсировано уменьшением гравитационной энергии связи между галактиками, что можно сделать только увеличив расстояние между галактиками R.
Упростим задачу, положив что обе галактики абсолютно одинаковы, то есть они имеют одинаковые массы и внутренние энергии гравитационной связи у них
одинаковы и одинаково изменяются во времени. Тогда написанная выше формула упростится до следующего вида
Далее из нее запишем формулу для баланса гравитационной энергии связи для двух значений E1 > E2
откуда получим
обозначим
и, в итоге получим
Из полученного уравнения видно, что если бы увеличение гравитационной энергии связи в галактиках было бы постоянным, то
скорость их разбегания была бы пропорциональна квадрату расстояния между ними. В то время как в законе Хаббла она пропорциональна
только первой степени расстояния. Найдем уравнение для изменения скорости увеличения гравитационной энергии связи, при котором выполнялся бы
закон Хаббла. Исходя из закона Хаббла запишем дифференциальное уравнение
Решая это дифференциальное уравнение находим функцию, описывающую изменение расстояния во времени
Тогда скорость и ускорение будут описываться следующими функциями
Из полученных уравнений находим, что для того, чтобы выполнялся закон Хаббла, скорость увеличения гравитационной энергии
связи материи в галактиках должна убывать по экспоненте